Simulation Islands
Island management is a fundamental low level feature of physics engines and can have a big impact on solver design and performance. This was one of the first problems I decided to work on for Box2D version 3 (v3).
Since I began working on v3 I’ve been comparing several algorithms for island management. My goal has been to make island building scale better with multiple CPU cores. Here are the three approaches I’ve considered:
- Depth-first search (DFS)
- Parallel union-find
- Persistent islands
Let’s dive in!
What are islands?
You can view a rigid body simulation as a graph where bodies are nodes and constraints are edges. Constraints consist of contacts (shapes touching) and joints (hinges, sliders, etc). From the graph point of view contacts and joints are the same.
In graph theory islands are called connected components. In rigid body simulation static bodies are not part of the graph. For example, this image shows three islands.

Static bodies are not part of the island graph because they can be shared among multiple islands. They need to shared because in a video game lots of bodies will be touching the static ground. Without sharing the static bodies among multiple islands there will be far fewer islands. Islands then lose their value. Islands are not required for correctness. They are an optimization (as we shall see) and they only work well as an optimization if there are many islands. Static bodies can be shared because nothing in the simulation affects their position or velocity. Sharing static bodies among multiple islands requires a little bit of care in the algorithms, but this is straight forward and for simplicity I will not include such logic in my examples.
In practice an island is a data structure that keeps track of a set of bodies and a set of constraints. This is the island data structure in Box2D v2.4:
class b2Island
{
b2Body** bodies;
b2Contact** contacts;
b2Joint** joints;
int bodyCount;
int contactCount;
int jointCount;
};Users of Box2D don’t interact with islands. They are an implementation detail of the solver. Box2D v2.4 does not retain islands across time steps, so there is no way to access them.
Sleeping and waking
Islands are very useful in game physics. The most important aspect is sleeping. Sleeping rigid bodies are removed from the solver and this drastically reduces their CPU load. The engine checks islands during simulation for low energy. If all bodies in an island have low energy for several time steps, then all the bodies in the island are flagged as sleeping and no longer added to the active simulation. The Box2D debug display shows sleeping bodies as gray.
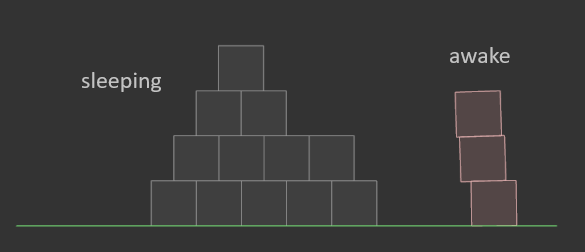
Sleeping must be done per island, not per body. I made this mistake early in my work on game physics. If you put a body to sleep but not the whole island then you will see shapes begin to overlap and joints begin to dislodge.
Sleep has a flip side as well: waking.
Bodies wake other sleeping bodies through constraints and this must propagate through all touching bodies immediately. Otherwise you get those nasty overlapping shapes and dislodged joints. Islands are just as important for waking as for sleeping.
Parallel islands
Islands work well for multicore simulation. Game worlds often have many separate islands of bodies. A ragdoll over here. A pile of debris over there. This relates to the concept of spatial coherence as described by Gino van den Bergen in his book Collision Detection in Interactive 3D Environments. Spatial conherence says that rigid bodies tend to spread out and we can take advantage of this to improve performance and lower memory usage.
An island can be simulated indepedently from other islands. Therefore an island can be simulated on a thread and you can send multiple islands to multiple threads using a task system such as enkiTS. This scales very well with CPU core count as long as there are a sufficient number of islands. This is also cache efficient because the core is doing significant work on a subset of the simulation world.
Parallel islands simulation is not a silver bullet. There may not be enough islands to span all the CPU cores. In some games there may be a large pile or tower of rigid bodies that are in a single island. This large single island can dominate performance even with multithreading. It can lead to a situation where many cores are sitting idle. I plan to discuss large islands in a future post.
 Large Island
Large Island
Depth-first search
Box2D v2.4 uses depth-first search DFS to build islands from scratch every time step. Version 2.4 does not have multithreading support, so islands are only used for sleeping and waking.
The SolveIslands function takes all the bodies and constraints of the simulation world and finds their simulation islands. Before finding the islands, it clears a mark (visitation flag) on every body and constraint. These marks ensure that a body or constraint is only added to a single island.
The algorithm has a simulation island G that is reused for each island found. The island finder loops over all bodies and looks for awake dynamic bodies to be the seed for the island. Starting from the seed, connected bodies and constraints are added to G. Once all the connected bodies have been traversed the island G is simulated, updating the constraint forces and the body velocities and positions. Then the algorithm continues looking for the next seed body that hasn’t already been simulated in the current time step.
function SolveIslands(bodies, constraints)
ClearMarks(bodies)
ClearMarks(constraints)
let G be an island
for seed in bodies
if seed not marked and seed is dynamic and seed is awake
Clear(G)
Mark(seed)
let S be a stack
S.Push(seed)
while S not empty
b = S.Pop()
G.Add(b)
for c in b.GetConstraints()
if c not marked
G.Add(c)
Mark(c)
other = OtherBody(c)
if other not marked
S.Push(other)
G.Simulate()
DFS has linear time complexity in the number of bodies. It can be made faster by only using awake bodies as seeds. This can be done by keeping an array of awake dynamic bodies.
Traversal mark management can also be expensive. At the cost of more memory, each body and constraint can hold a time step counter. The DFS can then compare a body’s time step counter with the current time step count of the physics world. Marking a body or constraint is done by setting the local time step counter equal to the world time step count.
The DFS naturally wakes bodies. When a body is added to an island it is flagged as awake. A body can only be flagged as sleeping with another routine called IslandSleep.
Part of island simulation is checking for sleeping. Every body has velocity and a sleep timer. If the velocity is greater than a velocity threshold then sleep timer is reset. Otherwise it is advanced by the time step. If the minimum sleep timer of all bodies in an island is greater than a time to sleep threshold then the entire island is marked as sleeping.
function IslandSleep(islandBodies, timeStep)
minSleepTime = MAX_FLOAT
for b in islandBodies
if b velocity > velocityThreshold
b.sleepTime = 0
minSleepTime = 0
else
b.sleepTime += timeStep
minSleepTime = Min(minSleepTime, b.sleepTime)
if minSleepTime > timeToSleep
for b in islandBodies
MarkSleeping(b)
Then the next time step no collisions between sleeping bodies are updated and sleeping bodies are not added to simulation islands unless an awake body begins interacting with a sleeping body. This is a huge win for performance in large game worlds.
Watch this video if you want more details on DFS:
Union-find
Union-find (UF) is a competitor to DFS for game physics island simulation. This algorithm is also called a Disjoint-set data structure.
UF focuses on merging sets (islands). Each dynamic body starts alone in its own set. As constraints are added to the world the sets are merged. Within each set a single body is considered the root body and uniquely identifies the set. After all constraints have been added the union-find is complete.
This video series explains union-find very well: https://youtube.com/playlist?list=PLDV1Zeh2NRsBI1C-mR6ZhHTyfoEJWlxvq&si=brluQ5CldgIXFMhv. If you are not familiar with union-find and/or path compression, please go watch this and come back.
Like DFS, union-find (with path compression) has linear time complexity for building islands. Union-find can be a drop-in replacement for DFS. However, some additional care must be used to ensure that all touching bodies are woke up.
The Amdahl problem
DFS and UF are fast but they are not parallel algorithms. So when I began multithreading Box2D I started to get timing results like this:
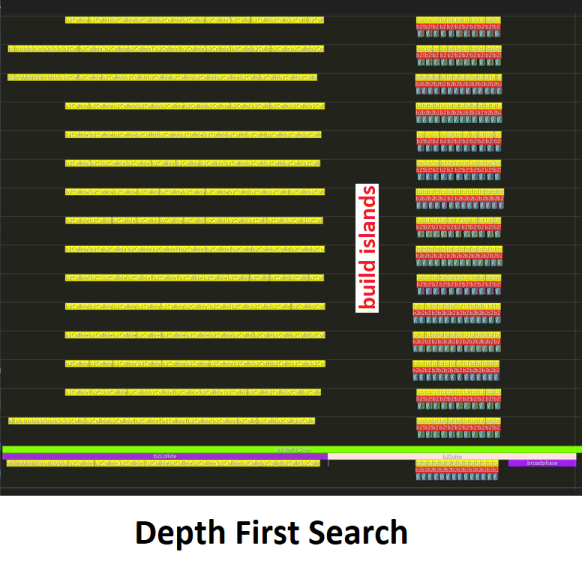
This is Amdahl’s law in action. Multi-core scaling is limited by single-threaded processing. You will also notice a single-threaded broadphase section which I’ll discuss in a future post.
Parallel union-find
At the GDC 2022, Jorrit Rouwe introduced a parallel union-find algorithm. The slides are here. You can also find an implementation in Jolt Physics.
I implemented this algorithm in Box2D v3. In the process I learned a lot about using atomics and lock-free algorithms. If you want to learn more about atomics and the C/C++ memory model, I highly recommend this two-part video by Herb Sutter:
The first challenge I faced was making the algorithm recursive so that it would wake entire islands in one time step. I needed to add some additional iteration to ensure that all touching bodies are woken up. After fumbling with atomics a bit, I got something working.
However, I quickly ran into a problem and did a lot of head scratching trying to figure out the problem. Fortunately I still have plenty of hair.
Parallel union-find uses atomic compare-and-swap (CAS) when merging islands. This means the order of constraints in the resulting islands is non-deterministic. The final order depends on which core happens to be faster at completing the CAS. This can change dramatically across time steps and repeated runs of the application.
This is a serious problem for the solver used in game physics because the constraints are solved one at a time, sequentially. The results from each constraint propagate to the next constraint. This contraint solver algorithm is formally called the Gauss-Seidel method. The problem is magnified because Box2D uses warm starting for contacts, which gets confused when the contraint order varies each time step. You can read more about Gauss-Seidel and warm starting here.
The constraints can be sorted after union-find and they can be sorted for each island independently. However, I could not find a faster way to do this than by using quicksort which is O(n log n). For large islands this added cost is significant, even when sorting a minimal index array. This video shows the effect of a parallel union-find and the resulting non-deterministic constraint order.
The serial DFS and UF do not have this problem. They generate constraints in a deterministic order. The loss of determinism is due to multithreading and the use of atomic CAS. If you want to learn more about determinism and multithreading, I recommend this video:
What’s next?
After implementing the parallel union-find I took a step back and reconsidered my options and tried to look at the big picture.
First, I decided that I did not want to sacrifice determinism. As a programmer I value predictability in the software I write. Determinism affects my ability to debug and any Box2D user’s ability to debug. I’m willing to give up performance for my software to be debuggable.
Second, Amdahl says that the serial part of a program dominates scaling. However, having a very fast serial part might be okay. Not every algorithm needs to be parallel if it is fast enough. So maybe I can find something faster than DFS or serial UF.
Third, Gino also describes temporal coherence in his book. Temporal coherence says the configuration of rigid bodies in a simulation does not change much across a single time step. How often do islands change? I suspect islands change slowly.
Fourth, maybe the cost of islands can be spread out in other ways. For example, it is urgent that islands are merged within the current time step. This is necessary to wake islands immediately. On the other hand it is not urgent to put islands to sleep or to split islands when bodies stop interacting. Delayed sleep is a minor performance loss.
Persistent islands
The points above led to me investigate persistent islands. Persistent islands are retained across time steps. They need to support adding and removing bodies and contraints incrementally.
When a dynamic body is created it also creates a new island: an island of a single body. Static bodies do not get islands.
When a constraint between two dynamic bodies is created the two associated islands are merged. It may be the case that the bodies are already in the same island and this is an early out in the island merger.
When a dynamic body is destroyed it is removed from its island. If that island is now empty then the island is also destroyed.
When a constraint is destroyed then it is removed from the island. The island becomes a candidate for splitting.
I need to merge persistent islands immediately. This is necessary to ensure that all bodies that should be awake are added to the active simulation.
Persistent island splitting can be deferred. I can put a quota on island splitting. For example, one island per time step can split. Maybe I can choose to split the largest island first. Or maybe I can choose to split the island with the most constraints removed. Some heuristic can be used. I suspect any reasonable heuristic is fine.
I modified the v2.4 island structure to support adding and removing bodies and constraints quickly using linked lists. This also makes it fast to merge islands. Linked lists are slow to traverse because of cache misses, but I suspect I will not need to traverse them often. I also added a flag maySplit to indicate that the island has had contacts or joints removed and it may be possible to split the island into two or more islands.
struct b2Island
{
int index;
int parentIsland;
int headBody;
int tailBody;
int headContact;
int tailContact;
int headJoint;
int tailJoint;
bool maySplit;
};If I have an existing set of islands I can add an edge and this may lead to two islands merging. Island merging should be fast and it has to be deterministic. I decided to stick with serial union-find for merging islands.
Here is the code for adding a contact constraint. Joints are similar. I abbreviated the code a bit and left out path compression. You can see the full version here. Notice that islands are flagged as awake when they are merged.
void b2LinkContact(b2Island* islands, b2Body* bodyA, b2Body* bodyB, b2Contact* contact)
{
int islandIndexA = bodyA->islandIndex;
int islandIndexB = bodyB->islandIndex;
if (islandIndexA == islandIndexB)
{
// bodyA and bodyB are already in the same island
b2AddContactToIsland(&islands[islandIndexA], contact);
return;
}
// Find root of islandA
b2Island* rootA = &islands[islandIndexA];
b2WakeIsland(rootA);
while (rootA->parentIsland != B2_NULL_INDEX)
{
rootA = &islands[rootA->parentIsland];
b2WakeIsland(rootA);
}
// Find root of islandB
b2Island* rootB = &islands[islandIndexB];
b2WakeIsland(rootB);
while (rootB->parentIsland != B2_NULL_INDEX)
{
rootB = &islands[rootB->parentIsland];
b2WakeIsland(rootB);
}
// Make islandB a child of islandA
if (rootA != rootB)
{
rootB->parentIsland = rootA->index;
}
b2AddContactToIsland(rootA, contact);
}Removing a contact from an island involves linked list bookkeeping and flagging the island for spitting (maySplit). Union-find is not involved.
Once all the new constraints have been added to all islands, there is a serial merge step. Here is an abbreviated version of the code. The full version is here. The function b2MergeIslandWithParent is just some boring bookkeeping code. Note that b2DestroyIsland invalidates the current island, so tread carefully.
void b2MergeIslands(b2Island* islands, int count)
{
// Step 1: ensure every child island points directly to its root island
for (int i = 0; i < count; ++i)
{
b2Island* island = &islands[i];
b2Island* rootIsland = island;
while (rootIsland->parentIsland != B2_NULL_INDEX)
{
rootIsland = &islands[rootIsland->parentIsland];
}
if (rootIsland != island)
{
island->parentIsland = rootIsland->index;
}
}
// Step 2: merge every awake island into its parent
for (int i = 0; i < count; ++i)
{
b2Island* island = &islands[i];
if (island->parentIsland != B2_NULL_INDEX)
{
b2MergeIslandWithParent(island);
b2DestroyIsland(island);
}
}
}These code snippets show that union-find builds multiple island trees then collapses each island tree into its root island. With persistence this process can occur incrementally as shapes come into contact.
Island splitting
I handle island splitting by taking an island and using all of its bodies as seeds for the DFS algorithm. This could be done with union-find as well. Any island finding algorithm will do. I’m not really splitting the island, I just building new islands from the original island.
Because the island is guaranteed not to connect to other islands, the depth-first traversal is guaranteed to stay within the original island. This is critical to allow the original island to be split concurrently with other work.
Here is the pseudo-code for island splitting. It is very similar to the DFS algorithm above. Instead of dealing with all the bodies and constraints in the entire simulation world, it is limited to the bodies and constraints of a single island. After a new island is built, it is added to the world as a new persistent islands. After the island is split the original island is destroyed. This is fine because nothing should refer to the original island at this point.
function SplitIsland(world, island)
bodies = GetIslandBodies(island)
constraints = GetIslandConstraints(island)
ClearMarks(bodies)
ClearMarks(constraints)
let G be an island
for seed in bodies
if seed not marked and seed is dynamic and seed is awake
Clear(G)
Mark(seed)
let S be a stack
S.Push(seed)
while S not empty
b = S.Pop()
G.Add(b)
for c in b.GetConstraints()
if c not marked
G.Add(c)
Mark(c)
other = OtherBody(c)
if other not marked
S.Push(other)
world.AddIsland(G)
world.DestroyIsland(island)
The result of splitting the island is one or more new islands. It is a little sad if only one new island results, but it would be the correct result. Removing a constraint may or may not cause and island to split into two islands. Determining whether an island will split or not is similar to the work of doing the DFS, so I might as well optimistically attempt to split the island.
Making persistent islands fast
While working on parallel union-find I learned that the narrow-phase can drive island management. The narrow-phase is the simulation stage where contact points are computed between colliding shapes. The contact pairs that manage potentially colliding shapes are persisted across time steps. Each contact pair holds the current contact points. The number of contact points is 0, 1, or 2. If the number of contact points changes from zero to non-zero or vice-versa then there is an edge that should be added or removed from the island graph.
Scalability requires the narrow-phase to be executed in parallel. This is a naturally parallel algorithm because the contact points between one shape pair are not affected by other shape pairs. This is the easiest part of a physics engine to spread across multiple cores. Like butter on bread.
When a contact pair is updated there are three outcomes relevant to persistent islands:
- edge added
- edge removed
- unchanged
The gambit is that most pairs fall in the third camp in a typical game scenario. This seems to be the case so far in my testing.
Edge additions need to be processed right away, before the islands are solved. I handle this with serial union-find as described above. Edge removals are less urgent. The contact constraint needs to be removed right away, but the island doesn’t need to be split. Removing and edge doesn’t mean the island will split. There may be other edges holding the island together. However, the island might split. So I flag the island as potentially splitting.
I can defer island splitting to later. For example, I can split an island after it has been solved, in the same task. This works because island A doesn’t care if island B is split. Island A only cares if island B wants to merge with it. And merging is handled serially.
How about determinism? Determinism is maintained if the edge additions and removals are processed in deterministic order. It turns out in Box2D that the order of contact pairs in the world is deterministic, so I just need to process the edge changes according to the order of the contact pairs. However, there can be a huge number of contact pairs and looping over all the pairs serially looking for changes is going to be very slow.
There is one data structure that can have an large number of entries and still be fast to iterate across. The bit array! Modern CPUs help us do this quickly with bit scanning intrinsics. See this and this.
The bit array can also work well with multithreading. Each narrow-phase worker can access a thread context that holds a local bit array. When the contact pair has an edge add or remove outcome, it flips a bit in the thread context bit array. Then after the narrow phase is complete, the main thread can bit-wise OR all the bit arrays together. This is quite fast using a bit array built on 64-bit words. And no atomics are needed.
Putting this all together I have the program flow shown below. This example has three threads in the narrow phase. Each thread gets its own bit array which is initially all zeros. When a contact pair is processed it checks if the number of contact points went from 0 to non-zero or vice-versa. In either case it sets the thread’s bit array at the index associated with the contact pair. After all contact pairs are processed the bits from each thread are combined into a global bit array using bit-wise OR. Then a loop iterates over the global bit array looking for set bits. If a set bit is found, the code looks up the contact pair and determines if an edge should be added or removed from the island graph and then does that work. These additions and removals are done serially in the main thread. This retains a deterministic constraint order.

In practice the number of set bits is very small. Bit traversal is very fast, even for a large number of contact pairs.
Results
And performance? Performance is good. Gino was right!
This image shows a typical timing result. The blue bars are the contact pairs and the yellow bars are the island constraint solvers. The gap in between is the serial island management. The gap also includes island solver preparation and task system overhead.

Let’s look at some benchmarks.
The first test is 182 pyramids with a base of 10 boxes, so 55 bodies each and a total of 10010 bodies. These pyramids are not moving and so this test favors persistent islands.

The tumbler test has 2000 boxes inside a hollow box that is constantly rotating on a revolute joint. This test should be difficult for persistent islands because constraints are constantly being added and removed. The darker boxes are colored that way because Box2D considers them fast enough to engage continuous collision checks.

Here are the results for the two tests. Times are in milliseconds. The first time value is the average and the value in parentheses is the maximum. For DFS I’m using commit #32 of Box2D v3. For persistent islands I’m using commit #36.
For persistent islands there can be many frames in a row where the island management has no work, making it tricky to benchmark. Persistent islands are strangly fast. I had to verify the code was working a few times. Indeed it is doing real work as I have tested island merging and splitting as well as sleeping and waking.
Take the maximums with a grain of salt. They could be due to anything. I include them because the persistent island has a heavier load when the bodies are created and this is relevant to avoid frame rate dips.
| Test | DFS | Persistent |
|---|---|---|
| pyramids | 0.69 (0.98) | 0.01 (0.45) |
| tumbler | 0.43 (0.87) | 0.08 (0.43) |
Persistent islands are roughly an order of magnitude faster than DFS.
What about splitting?
The current implementation uses DFS to split at most one island per time step. My current heuristic is to split the largest island that has had one or more constraints removed.
Island splitting isn’t free but it is usually easy to hide the cost. I have experimented with putting the island splitting at the end of an island solve task. When there are many islands and multiple cores then this time is almost completely hidden and insignificant, amounting to a few microseconds on a single core.
If there are a small number of large islands then the cost of splitting can be significant. Nevertheless, island splitting can be done in parallel with other work and this is a significant gain over the traditional serial DFS/UF.
Summary
I covered a lot of material in this post and there are a lot of references and auxilliary knowledge. Simulation islands touch a lot of systems, so it is challenging to fully understand islands without understanding how a physics engine is put together. Hopefully I’ve provided enough background knowledge so you can understand the scope of island mangement. If not, please let me know!
These are the main takeaways I have learned or reinforced while working on islands:
- island management can become a bottleneck in multicore simulation
- determinism is important for game physics
- spatial and temporal coherence provide many opportunities for improving performance
- sometimes a fast serial algorithm may be better than a parallel algorithm
- bit arrays are awesome!
What’s next?
At the end of this journey I have many tools to work with islands. This will help me as I explore other aspects of improving Box2D.
There is more work to do on Box2D and more to write up. I plan to post more in the future on broad-phase improvements and dealing with large islands. Stay tuned!
I’d like to add that Jolt is a fantastic physics engine and Jorrit has done amazing work. Parallel union-find is an ingenious algorthim and is useful in some situations. I have learned a lot looking at Jolt and found several treasures in Jorrit’s code. I’ll share more in the future.
4428 words
2023-10-07 17:00 -0700
